Modelo matemático de aprendizado de máquina
(Uso do algoritmo Perceptron no campo da inteligência artificial do aprendizado supervisionado)
Exemplo:
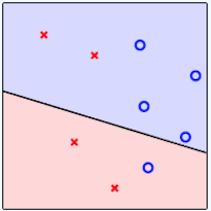
Dado um conjunto de dados linearmente separáveis em 2 dimensões por uma reta,
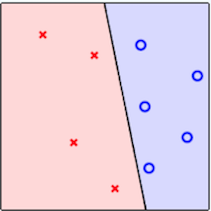
ajustar a reta até que torne os dados perfeitamente separáveis.
| 
| 
|
| Dados não classificados
| Dados Classificados
| Matriz dos dados
|
Formula:
h(x)=sign((\sum_{i=1}^d w_i x_i)+b)
onde:
Saida:
s;&space;: vetor de saída
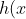&space;=&space;\left&space;\{&space;\begin{matrix}&space;sim,&space;&&space;\mbox{se&space;}h=\mbox{&space;+1}\quad&space;atingiu&space;\quad&space;alvo&space;\\&space;n\tilde{a}o,&space;&&space;\mbox{se&space;}h=\mbox{-1}&space;\quad&space;n\tilde{a}o&space;\quad&space;atingiu&space;\quad&space;alvo&space;\end{matrix}&space;\right&space;\quad)
Entrada:
x_1,...,x_n;&space;são dados de coletados e trnsformados em 1 e -1 da entrada.
sign = \left \{ \begin{matrix} +1, & \mbox{se }sign>0 \quad indica \quad presença \quad de \quad uma \quad caracteristica \mbox{ } \\ -1, & \mbox{se }sign<0 \quad indica \quad ausencia \quad de \quad caracteristicas \mbox{ } \end{matrix} \right
Parâmetros:
w_1,...,w_n \quad :s\tilde{a}o \quad pesos \quad a \quad serem \quad ponderados (s\tilde{a}o \quad parametros \quad a \quad serem \quad treinados).
d:significa dimensão ou seja números de planos lineares
b: desloca a reta da origem (bias- significa o limite em que a reta será inclinada). Se b=0 a reta esta na origem.
Algoritimo de aprendizado:
Importante:
- Não ocorre variação do peso se a saida estiver correta.
- caso contrario, cad peso é incrementado de η quando a saida
é menor que o alvo (tartget) t é decrementado de η quando
a saída é maoior que o alvo.
- iniciar os pesos com valores randomicos e
pequenos ou iguais a zero;
- aplicar um padrão com seu respectivo valor desejado de saída t_j&space;" > e verificar a saída da rede s_j&space;" >;
- calcula o erro na saída E_j&space;=&space;t_j&space;-&space;s_j" >;
- se E_j&space; = 0, volta ao passo 2;
se E_j&space; ≠ 0, atualiza os pesos: ∆ w_i_j&space;= η x_iE_j;&space;
- volta ao passo 2.
Processo de aprendizado:
Exemplo:
Dados de entrada
x
Parametros
w
b
Resultados
Implementação em python:
Dados Teste
Resultado
Referências:
- Abu-Mostafa,.... Learning from data. A short course
- https://pt.wikipedia.org/wiki/Ajuda:Guia_de_edição/Fórmulas_TeX
- pt.wikibooks.org/wiki/Ajuda:Marcação_TeX#Sintaxe
-
codigo de caracteres html5
editor de formulas
-
latex
Uso do latex:
x\in\mathbb{N}\subset\mathbb{Z}\subset\mathbb{R}\sub\mathbb{C}
{\color{Blue}x^2}+{\color{YellowOrange}2x}-{\color{OliveGreen}1}
ƒn=ƒn-1+ƒn-2 onde ƒ0=1 e ƒ1=1



