Modelagem matemática, aprendizado supervisionado de uma máquina de estados (autômata) de um sistema de informação
por Walter Dominguez (Fgv-Emap)
TrabEmapHist.html
2017
Objetivo Pessoal:
Busca de um foco em aprendizado de máquina.
Meta Pessoal:
Revitalizar mestrado através de curso e trabalhos até que tenha um objetivo pessoal claro.
Atividade Pessoal:
Coletar informação e fazer resumo com foco na analise de dados para definir objetivo.
Estratégia consolidar analise dados, inteligência coletiva e rede neural.
Tarefa Pessoal:
Rever site pessoal
Curso análise de dados.
Curso Algebra??? e outros??.
Resumo:
Treinamento supervisionado de uma rede de conhecimento neural (já se sabe o resultado) do algoritmo "perceptron"
(1º algoritmo a se baser no funcionamento do cérebro humano).
Uso e motivação:
Para o analista e engenheiro de sistema, matemático, estatístico, cientista de dados, programador e tutor que necessitem de revisar os conceitos e processo em modelagem matemática, aprendizagem de máquina, mineração de dados e visualização de dados, tendo como apoio a ciência da computação e informação, estatística, algebra e treinamento de algoritmos..
Este estudo pode ser replicado com adaptações para outras aplicações de classificações.
O objetivo deste estudo é prospectar meus conhecimentos para leitura, interpetração e visualização dos números.
Abordagem do trabalho:
-
Coleta inicial de informação visando obter / adequar o objetivo, escopo e como chegar a êles, a partir da solução desejada.
Estrutura do trabalho:
1. Introdução
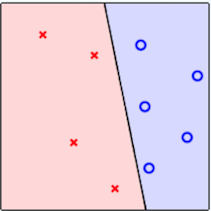
Mostrar seres vivos separando
bípede (o) do
quadrúpede (*) por uma reta ajustável.
|
|
<== |
cão
gato
cavalo
homem
galinha
avestruz
|
[ 1-1 1 1 ]
[ 1 1 1 1 ]
[ 1 1-1 1 ]
[-1-1-1 1 ]
[-1 1-1 1 ]
[ 1-1 1-1 ]
|
1
1
1
-1
-1
-1
|
<== |
 |
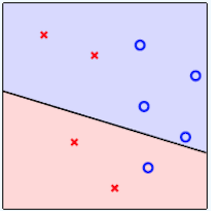
Dados Classificados
x e o aparecem separados
Visualização da Saida |
Dados não classificados
x e o aparecem misturados
Visualização da Entrada |
|
entrada
|
|
resultado
esperado
|
|
Seres vivos aparecem
misturados
Visualização do Ambiente |
voltar ao topo
2. Método para fazer classificação (partindo da equação alvo escolhida)
| visualização
entrada
|
|
modelo
matemático
(equação alvo)
|
|
modelo de
informação
|
|
visualização
modelo de
claasificação
com erro
|

|
==>
|
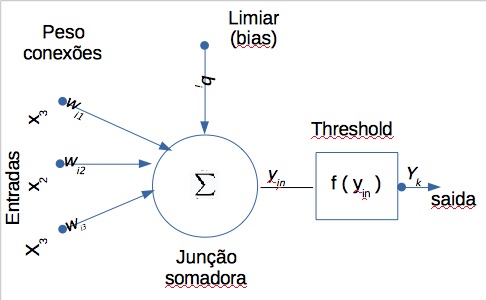
s(x)=sign((\sum_{i=1}^d w_i x_i)+b)
onde:
s(x) : saida da função (pode ser +1 ou -1).
x: vetor de entrada com dados.
para o treinamento
w: peso a ser achado.
b: limite a ser variado (inclinação da reta)
|
==>
|
|
==>
|

|
|
modelo de
claasificação
com erro
|
|
modelo
matemático
do erro.
|
|
modelo de
informação
|
|
visualização
modelo de
claasificação
|

|
==>
|
e_j(t) = d_j(t)-y_j(t)
w(j)=\\ \sum_{0}^{len(w)}w_{j}+taxa \quad aprendizado+t_{i}*x_{ij}
b=b+taxa \quad aprendizado+t_{i}*x_{ij}
onde:
é o sinal observado.
na saida do neurônio j
no instante t. onde e_j(t)
é uma variavel aleatória.
|
==>
|

|
==>
|

|
voltar ao topo
3. Conjunto de entrada e saida
|
|
:Humano\quad&space;e\quad&space;Cavalo\quad&space;(matriz\quad&space;treinamento)\\&space;Caracteristicas\quad(coluna):\\&space;..|ser&space;\vivo&space;(possui&space;\quad&space;DNA)\quad&space;para\quad&space;diferenciar\quad&space;do\quad&space;robo\\&space;..........|b\acute{i}pede\quad&space;tem\quad&space;4\quad&space;pernas\\&space;...............|quadr\acute{u}pede&space;\quad&space;tem\quad&space;2&space;\quad&space;pernas\\&space;..|.......|....|\\&space;\quad)
|
| bípede
|

|
| quadrúpede
|
| Matriz dos dados entrada.......algoritmo........Matriz dos dados saida
|
|
3.1 Saida esperada:
s;&space;: vetor de saída
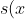&space;=&space;\left&space;\{&space;\begin{matrix}&space;sim,&space;&&space;\mbox{se&space;}s=\mbox{&space;+1}\quad&space;atingiu&space;\quad&space;alvo&space;\\&space;n\tilde{a}o,&space;&&space;\mbox{se&space;}s=\mbox{-1}&space;\quad&space;n\tilde{a}o&space;\quad&space;atingiu&space;\quad&space;alvo&space;\end{matrix}&space;\right&space;\quad)
3.2 Entrada:
Vetor de entrada:
x_1,...,x_n;&space;são dados de coletados e trnsformados em 1 e -1 da entrada.
Significado do conteudo de entrada :
sign = \left \{ \begin{matrix} +1, & \mbox{se }sign>0 \quad indica \quad presença \quad de \quad uma \quad caracteristica \mbox{ } \\ -1, & \mbox{se }sign<0 \quad indica \quad ausencia \quad de \quad caracteristicas \mbox{ } \end{matrix} \right
Exemplo:\&space;x_1=[1\&space;1 -1] \&space;\&space; x_2=[1 -1\&space;1]
3.3Parâmetros:
w_1,...,w_n \quad :s\tilde{a}o \quad pesos \quad usados \quad na \quad ponderação (s\tilde{a}o \quad parametros \quad a \quad serem \quad treinados).
d:significa dimensão ou seja números de planos lineares
b: desloca a reta da origem (bias- significa o limite em que a reta será inclinada). Se b=0 a reta esta na origem.
\eta&space;:&space;alvo.&space;\quad&space;Resultado&space;\quad&space;esperado"
\&space;Threshold:&space;\quad&space;limite &space;\quad&space;de&space;\quad&space;saida"
voltar ao topo
4. Arquitetura da rede:

- O objetivo desta rede é classificar alguns padrões de entrada como pertencentes ou não a uma classe.
- Considerar o conjunto de dados de entrada como
sendo formado por N amostras
\left\{x_1,d_1\right\},\left\{x_2,d_2\right\},...,\left\{x_n,d_n\right\}, onde x_j&space; é o vetor j de entradas, ed_jsua saida desejada(classe) correspondente.
voltar ao topo
5. Interpretação geométrica da eq. y_i=w_ix_i + b&space; :
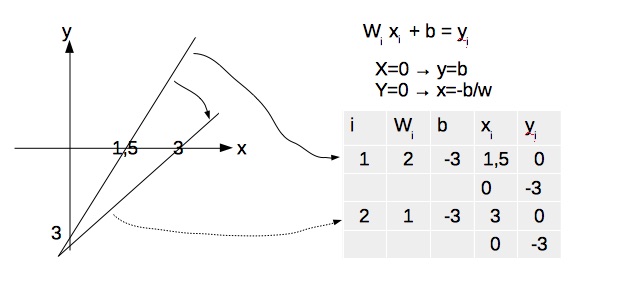
- Considere o problema de utilizar o perceptron com um único neurônio para representar a função lógica AND..
- A saida y_i do neorônio para o vetor de dados x_i pode ser representada na forma:
y_i=f(w_ix_i + b)
- Para quaisquer valor de w e b, a função f(u) separa o espaço de entrada em duas regiões, sendo que a curva de separação (superficie de decisão) é uma linha reta.
-
A equação desta reta é dada por:
w_1x_1+w_2x_2+b = 0
-
Se a função de ativação do tipo sinal(degrau) possui θ = 0, então:
w_1x_1+w_2x_2+b ≥ 0
Resultará uma saida positiva da rede.
- Considere, como 1a hipótese: w_1 = 2; b = -3, y_1=0 \rightarrow x_1=1,5 e x_1=-3 \rightarrow y_1=-3 .
- Considere, como 2a hipótese: w_2 = 1; b = -3, y_2=0 \rightarrow x_2=3 e y_2=0 \rightarrow x_2=3
- a figura mostra as duas superficies de decisão e os pesos e bias determinados pelo algoritimo de treinamento do perceptron.
voltar ao topo
6. Algoritimo de aprendizado:
Formato de fluxo:
 Formato de expressão matemática
Formato de expressão matemática
\Delta=\eta x_ie_j;&space;
- Não ocorre variação do peso se a saida estiver correta.
- caso contrario, cada peso é incrementado de η quando a saida
é menor que o alvo (tartget) t é decrementado de η quando
a saída é maior que o alvo.
Formato descritivo:(passo a passo)
- iniciar os pesos com valores randomicos e
pequenos ou iguais a zero;
- aplicar um padrão com seu respectivo valor desejado de saída t_j&space;" > e verificar a saída da rede s_j&space;" >;
- calcula o erro na saida E_j=t_j-Sj;
- se E_j&space; = 0, volta ao passo 2;
se E_j&space; ≠ 0, atualiza os pesos: \Delta w_i_j&space;= \eta x_iE_j;&space;
- volta ao passo 2.
Formato pseudo-código estruturado:
![\\\mathbf\\ \mathbf{procedure} [w]:perceptron(maxIt,E,\alpha,\mathbf{X},\mathbf{d}) \\ Inicialize \ w\ //\ inic \ com\ 0 \\ Inicialize \ b\ //\ inic \ com\ 0 \\ t\leftarrow 1\\ \mathbf{while} \ t< maxIt\ AND \ E> 0 \ do,\\ \quad \quad \mathbf{for}\ i \ from \ 1 \ to \ N \ do, \\ y_i \leftarrow f(wx_i + b)\\ e_i \leftarrow d_i - y_i\\ w \leftarrow w+\alpha e_ix_i\\ b\leftarrow b+\alpha e_i\\ \mathbf{end}for\\ E \leftarrow sum(e_i)\\ t \leftarrow t +1\\ \mathbf{end} while\\ \mathbf{end} procedure \quad](https://latex.codecogs.com/gif.latex?\\\mathbf\\&space;\mathbf{procedure}&space;[w]:perceptron(maxIt,E,\alpha,\mathbf{X},\mathbf{d})&space;\\&space;Inicialize&space;\&space;w\&space;//\&space;inic&space;\&space;com\&space;0&space;\\&space;Inicialize&space;\&space;b\&space;//\&space;inic&space;\&space;com\&space;0&space;\\&space;t\leftarrow&space;1\\&space;\mathbf{while}&space;\&space;t<&space;maxIt\&space;AND&space;\&space;E>&space;0&space;\&space;do,\\&space;\quad&space;\quad&space;\mathbf{for}\&space;i&space;\&space;from&space;\&space;1&space;\&space;to&space;\&space;N&space;\&space;do,&space;\\&space;y_i&space;\leftarrow&space;f(wx_i&space;+&space;b)\\&space;e_i&space;\leftarrow&space;d_i&space;-&space;y_i\\&space;w&space;\leftarrow&space;w+\alpha&space;e_ix_i\\&space;b\leftarrow&space;b+\alpha&space;e_i\\&space;\mathbf{end}for\\&space;E&space;\leftarrow&space;sum(e_i)\\&space;t&space;\leftarrow&space;t&space;+1\\&space;\mathbf{end}&space;while\\&space;\mathbf{end}&space;procedure&space;\quad)
voltar ao topo
7. Processo de aprendizado:
- Minimizar erro quadrático.
- Método do gradiente descendente.
\Delta w_i_j = -\eta \frac{\delta E }{\delta W_i_}
Simulador do Operador lógico AND
| AND
|
x0
|
x1
|
x2
|
t
|
| Entrada
1
|
1
|
0
|
0
|
0
|
| Entrada
2
|
1
|
0
|
1
|
0
|
| Entrada
3
|
1
|
1
|
0
|
0
|
| Entrada
4
|
1
|
1
|
1
|
1
|
|
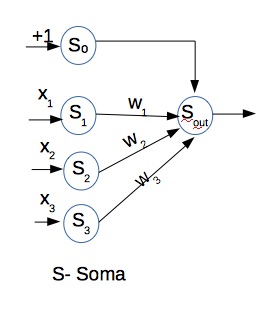
|
| Peso
inicial: w_0, wi=0, w2=0
|
| Taxa
de apredizado: n=0.5
|
|
ciclo1
Entrada 1: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+0\times0+0\times0)=f(0)=0 \rightarrow S_o_u_t=t
Entrada 2: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+0\times1+0\times0)=f(0)=0 \rightarrow S_o_u_t=t
Entrada 3: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+0\times0+0\times1)=f(0)=0 \rightarrow S_o_u_t=t
Entrada 4: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+0\times1+0\times1)=f(0)=0 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=0+0.5\times(1-0)\times1=0.5
w_1=w_1+\eta(t-S_o_u_t)x_1=0+0.5\times(1-0)\times1=0.5
w_2=w_2+\eta(t-S_o_u_t)x_2=0+0.5\times(1-0)\times1=0.5
ciclo2
Entrada 1: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0.5 \times 1+0.5\times0+0.5\times0)=f(0.5)=1 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=0.5+0.5\times(0-1)\times1=0.5
w_1=w_1+\eta(t-S_o_u_t)x_1=0.5+0.5\times(0-1)\times1=0.5
w_2=w_2+\eta(t-S_o_u_t)x_2=0.5+0.5\times(0-1)\times1=0
Entrada 2: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+0.5\times1+0.5\times0)=f(0.5)=1 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=0+0.5\times(0-1)\times1=0.5
w_1=w_1+\eta(t-S_o_u_t)x_1=0.5+0.5\times(0-1)\times1=0.5
w_2=w_2+\eta(t-S_o_u_t)x_2=0.5+0.5\times(0-1)\times1=0
Entrada 3: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-0.5 \times 1+0.5\times1+0\times0)=f(0)=0 \rightarrow S_o_u_t=t
Entrada 4: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-0.5 \times 1+0.5\times1+0\times1)=f(0)=0 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=-0.5+0.5\times(1-0)\times1=0
w_1=w_1+\eta(t-S_o_u_t)x_1=0.5+0.5\times(1-0)\times1=1
w_2=w_2+\eta(t-S_o_u_t)x_2=0+0.5\times(1-0)\times1=0.5
ciclo3
Entrada 1: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+1\times0+0.5\times0)=f(0)=0 \rightarrow S_o_u_t = t
Entrada 2: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(0 \times 1+1\times0+0.5\times1)=f(0.5)=1 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=-0.5+0.5\times(0-1)\times1=-1
w_1=w_1+\eta(t-S_o_u_t)x_1=1+0.5\times(0-1)\times0=1
w_2=w_2+\eta(t-S_o_u_t)x_2=0.5+0.5\times(0-1)\times1=0
Entrada 3: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times1+0\times0)=f(0)=0 \rightarrow S_o_u_t=t
Entrada 4: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times1+0\times1)=f(0)=0 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=-1+0.5\times(1-0)\times1=-0.5
w_1=w_1+\eta(t-S_o_u_t)x_1=1+0.5\times(1-0)\times1=1.5
w_2=w_2+\eta(t-S_o_u_t)x_2=0+0.5\times(1-0)\times1=0.5
ciclo4
Entrada 1: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-0.5 \times 1+1.5\times0+0.5\times0)=f(0.5)=0 \rightarrow S_o_u_t=t
Entrada 2: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-0.5 \times 1+1.5\times0+0.5\times1)=f(0)=0 \rightarrow S_o_u_t=t
Entrada 3: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-0.5 \times 1+1.5\times1+0.5\times0)=f(1)=1 \rightarrow S_o_u_t \neq t
w_0=w_0+\eta(t-S_o_u_t)x_0=-0.5+0.5\times(0-1)\times1=-1
w_1=w_1+\eta(t-S_o_u_t)x_1=1.5+0.5\times(0-1)\times1=1
w_2=w_2+\eta(t-S_o_u_t)x_2=0.5+0.5\times(0-1)\times0=0.5
Entrada 4: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times1+0.5\times1)=f(0.5)=1 \rightarrow S_o_u_t = t
ciclo5
Entrada 1: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times0+0.5\times0)=f(-1)=0 \rightarrow S_o_u_t=t
Entrada 2: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times0+0.5\times1)=f(0.5)=0 \rightarrow S_o_u_t=t
Entrada 3: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times1+0.5\times0)=f(0)=0 \rightarrow S_o_u_t = t
Entrada 4: S_o_u_t = f(w_0x_0+w_1x_1+w_2x_2)\\
=f(-1 \times 1+1\times1+0.5\times1)=f(0.5)=1 \rightarrow S_o_u_t = t
{\color{blue}w_0=-1, w1=1, w_2=0.5}
voltar ao topo
8. Implementação do algoritimo em python:
Foi utilizada a interface de desenvolvimento (IDE) Anaconda para editar o programa de implemtação na linguage Python 3.
voltar ao topo
9. Aplicações:
- Classificação de padrões.
- Clustering e Aproximação funcional.
- Série temporais.
- Otimização.
- Técnicas no prognóstico de mercados financeiros.
- Reconhecimento ótico de caracteres (OCR) .
- análise e processamento de sinais;
- controle de processos;
- robótica;
- classificação de dados;
- reconhecimento de padrões em linhas de montagem ;
- filtros contra ruídos eletrônicos;
- análise de imagens;
- análise de voz;
- avaliação de crédito;
- análise de aroma e odor- um projeto que está em desenvolvimento, buscando a análise de odor via nariz eletrônico;
- análise e diagnóstico de descargas parciais pelo reconhecimento do padrão acústico- trata-se de uma tese de mestrado cujo objetivo é criar um sistema com capacidades de classificar o padrão acústico de uma descarga parcial ;
voltar ao topo
10. Conclusões e próximos trabalhos:
- Redes de apenas uma camada só representa funções linearmente separáveis.
- Redes múltiplas camadas solucionam esta restrição.
- O desenvolvimento de algoritimos Back Propagation foi um dos motivos para o ressurgimeno da área de redes neuraos
voltar ao topo
11. Anexos
Voltado para infra estrutura de apoio ao trabalho como por exemplo: abordagem de trabalho, ferramentas, técnicas e conceitos.
voltar ao topo
11.2 Abordagem do trabalho
Inicialmente usar método da tentativa e erro a partir do problema resolvido (solução para os usuários do estudo).
Escrever o primeiro texto executando a solução imaginada.Ex: pegar um programa (ou algoritimo ou equação ou conceito) que já funciona e partir para sua especificação de requisito.
Através de estudos sucessivos ir melhorando a especificação até chegar a tópicos, consistentes, consolidados e integrados.
Adequar os objetivos e tópicos a cada revisão que geram consitência e integração entre tópicos .
O espaço entre ma revisão e outra deverá ter pelo menos uma noite no meio.
O objetivo, o escopo e como chegar a êle, deverá ser obtido/melhorado durante a fase inicial.
11.2 Notação Matemática
Função somatório
\sum_{i=1}^d w_i x_i \quad somat \acute{o} rio \quad do \quad elemento \quad i \quad do \quad vetor \quad w, \quad indexando \quad de \quad 1 \quad a \quad d \\ vezes \quad elemento \quad i \quad do \quad vetor \quad x, \quad indexando \quad de \quad 1 \quad a \quad d \\
ou \quad seja:
\quad w_1x_1+w_2x_2+w_3x_3+...+w_dx_d
11.3 Latex
11.4 Html usando latex
-
<left lang="latex">\sum_{i=1}^d w_i x_i </left> :
\sum_{i=1}^d w_i x_i
-
<left lang="latex">x\in\mathbb{N}\subset\mathbb{Z}\subset\mathbb{R}\sub\mathbb{C}> </left> :
x\in\mathbb{N}\subset\mathbb{Z}\subset\mathbb{R}\sub\mathbb{C}>
<left lang="latex">{\color{Blue}x^2}+{\color{YellowOrange}2x}-{\color{OliveGreen}1}>0 </left> :
{\color{Blue}x^2}+{\color{YellowOrange}2x}-{\color{OliveGreen}1}>0
voltar ao topo
11.5 Glossário
Focado ns revisão dos conceitos básicos de matemática, rede neuraL, automata, análise, estatística, hipertexto e aprendizado para obter resumo, consolidação e integração entre os tópicosMATEMÁTICA
CIÊNCIA DOS DADOS
Classe e atributo.
campo, variavel, caracteristicas(features)
Conjunto de dados.
vetor caracteristica, modelo,implementação do modelo, dimensão, esquema, amostra, exemplo, matriz confusão, valor ausente
Mineração.
De associação, de dados, limpesa e purificação de dados, validação cruzada
Classificação.
Classificador, cobertura, custo
Conhecimento.
KDD, descoerta do conhecimento
Aprendizado de maquinaMATEMÁTICA
Equações.
É igualdade envolvendo uma ou mais incógnatas.
O mundo das equações matemáticas
Expressão matemática.
É uma combinação de conjuntos de números, operadores, váriaveis, livres ou ligadas e simbolos gráficos({colchetes}, (parentes) e [chaves])
Lógica e Conjunto.
| implicação
lógica
|
==>
|
Inclusão
entre conjuntos
|
| Lógica
Implicação
|
|
Conjunto
Esta contido
|
|
|
|

|
Conjunto e proposição
Lógica e Conjunto
Conjunto de números
 Função.
É uma regra de relacionamento para mapeamento de um conjunto (domínio) em outro (contra domínio).
Função.
É uma regra de relacionamento para mapeamento de um conjunto (domínio) em outro (contra domínio).
 Elementos de uma função.
Domínio, contadomínio e imagem de uma função.
Elementos de uma função.
Domínio, contadomínio e imagem de uma função.
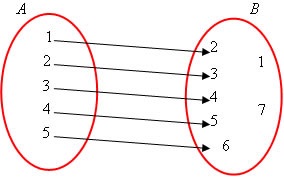 Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: sub conjunto de B que é representado pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
Tipos de função (classificação qto a imagem)
injetora ou injetiva - Um elemento do domínio corresponde a um e somente um do contradomínio (imagem). Ou seja todos o elementos do conjunto partida são utilizados
sobrejetora- dois elementos pode mapear 1 elemento do contradomínio.
bijetora - cada par do domínio corresponde a cada par do contradomínio.
* Não é uma função quando:
Não existe correspondência do elemento do dominio no contradomínio.
Um elemento do dominio mapea mais de um elemento no contra dominio.
* Todo elemento do domínio da função que tem como imagem o elemento 0, é uma raiz da função. É o lugar onda o grafico da função corta a abcissa.
Lista de funções.
Elementares
... Algébricas
........ Polimoniais
........... linear
........... quadrática
........... cúbica
........... quártica
........... quíntica
........... Racionais
........ Exponencial
........... raiz quadrada
... Transcesndentais
........ Exponencial
........ Hiiperbólica
........ Logaritimica
........ Periódica
........... trigonométrica
........... linear
Função reta.
Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: sub conjunto de B que é representado pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
Tipos de função (classificação qto a imagem)
injetora ou injetiva - Um elemento do domínio corresponde a um e somente um do contradomínio (imagem). Ou seja todos o elementos do conjunto partida são utilizados
sobrejetora- dois elementos pode mapear 1 elemento do contradomínio.
bijetora - cada par do domínio corresponde a cada par do contradomínio.
* Não é uma função quando:
Não existe correspondência do elemento do dominio no contradomínio.
Um elemento do dominio mapea mais de um elemento no contra dominio.
* Todo elemento do domínio da função que tem como imagem o elemento 0, é uma raiz da função. É o lugar onda o grafico da função corta a abcissa.
Lista de funções.
Elementares
... Algébricas
........ Polimoniais
........... linear
........... quadrática
........... cúbica
........... quártica
........... quíntica
........... Racionais
........ Exponencial
........... raiz quadrada
... Transcesndentais
........ Exponencial
........ Hiiperbólica
........ Logaritimica
........ Periódica
........... trigonométrica
........... linear
Função reta.
 Exemplo:
Exemplo:
 Função Erro quadrático
Limite de uma função
Dizemos que uma função f(x) tem um limite A quando x → a (→: tende), isto é, \lim_{x\rightarrow a}f(x)=A
Convergencia algoritmo
Distancia euclidiana
Algebra
Algebra e aplicações
Grafo
Grafos:Algoritmo e aplicação
Demostrações
Métodos:Direta, por contraposição, redução por absurdo,
Função Erro quadrático
Limite de uma função
Dizemos que uma função f(x) tem um limite A quando x → a (→: tende), isto é, \lim_{x\rightarrow a}f(x)=A
Convergencia algoritmo
Distancia euclidiana
Algebra
Algebra e aplicações
Grafo
Grafos:Algoritmo e aplicação
Demostrações
Métodos:Direta, por contraposição, redução por absurdo,
se e somente,
Métodos de demonstrações
Relacionamento de tópicos em matemática
 REDE NEURAL
Rede neurais artificiais(RNA): Trabalho de McCulloch e Pitts(1943).
De uma forma simplificada a RNA pode ser vista como um grafo onde os nós são os neurônios e as ligações fazem a função das sinapses (vávulas que controlam a trnsmissão dos impulsos entre os neurônios da rede).
História
43 - Trabalho de McCulloch e Pitts- simulação do funcionamento do celebro.
50-60 - Rosemblat(58)- apredizagem suoervisionada: perceptron.
69- Misky e Pappert - critica alimitações do perceptron. Pessimismo e dificuldade metodológica e tecnicas.
70 - Estacionário.
80 - interesse ressurgi, com aumento computacional e avanço metodológico.
Atual - http://playground.tensorflow.org . rede neural no Browse
http://scikit-learn.org/stable/modules/neural_networks_supervised.html . scikit learn rede neural
Modelo matemático dos neurônios
REDE NEURAL
Rede neurais artificiais(RNA): Trabalho de McCulloch e Pitts(1943).
De uma forma simplificada a RNA pode ser vista como um grafo onde os nós são os neurônios e as ligações fazem a função das sinapses (vávulas que controlam a trnsmissão dos impulsos entre os neurônios da rede).
História
43 - Trabalho de McCulloch e Pitts- simulação do funcionamento do celebro.
50-60 - Rosemblat(58)- apredizagem suoervisionada: perceptron.
69- Misky e Pappert - critica alimitações do perceptron. Pessimismo e dificuldade metodológica e tecnicas.
70 - Estacionário.
80 - interesse ressurgi, com aumento computacional e avanço metodológico.
Atual - http://playground.tensorflow.org . rede neural no Browse
http://scikit-learn.org/stable/modules/neural_networks_supervised.html . scikit learn rede neural
Modelo matemático dos neurônios
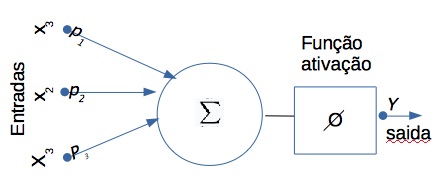 Um conjunto de n conexões (x_1, x_2,,...,x_n) que pode ser binária ou intervalar) associa os pesos (p_1, p_2,...,p_n).
Um acumulador \sum para realizar a soma ponderada de suas entradas.
Uma função de ativação \phi que limita o intervalo permissivel de amplitude do sinal de saida y a um valor fixo.
Tipos de RNA's:
Pela sua arquitetura (restringe o grupo de problemas) e é diferente pelo número de camadas (unica ou multiplas).
Pelo número de nós em cada camada, pelo tipo de conexão entre o nós (feedfoward ou feedback).
pela topologia: perceptron/adaline, backpropagation, hopfield, kohonen e art.
APRENDIZAGEM
Aprendizagem:
Uma das propriedades mais importantes da RN é a capacidade de aprender por meio de exemplos e fazer inferências sôbre o que aprenderam, melhorando gradativamente o seu desempenho.As RN utilizam um algoritimo de aprendizagem, cuja tarefa é ajustar as formas de conexões.
Aprendizado supervisionado:
Um agente externo(professor) apresenta a rede alguns conjuntos de padrões de entrada e saida.
Portanto é necessário ter um conhecimento prévio do que se deseja ou se espera da rede.
Para cada entrada o professor indica explicitamente se a resposta calculada é boa ou ruim.
A resposta fornecida pela rede neural é comparada a resposta esperada.
O erro verificado é informado a rede para que sejam feitos ajustes a fim de melhorar suas futuras respostas.
Exemplo.:
Aprendizado por Reforço:
para cada entrada apresentada, é produzida uma indicação (reforço) sobre a adequação das saídas correspondentes produzidas pela rede.
Aprendizado Não-supervisionado:
`A rede atualiza seus pesos sem o uso de pares entrada-saídas desejadas e sem indicações sobre a adequação das saídas produzidas.
AUTOMATA
Maquina de estado
Um conjunto de n conexões (x_1, x_2,,...,x_n) que pode ser binária ou intervalar) associa os pesos (p_1, p_2,...,p_n).
Um acumulador \sum para realizar a soma ponderada de suas entradas.
Uma função de ativação \phi que limita o intervalo permissivel de amplitude do sinal de saida y a um valor fixo.
Tipos de RNA's:
Pela sua arquitetura (restringe o grupo de problemas) e é diferente pelo número de camadas (unica ou multiplas).
Pelo número de nós em cada camada, pelo tipo de conexão entre o nós (feedfoward ou feedback).
pela topologia: perceptron/adaline, backpropagation, hopfield, kohonen e art.
APRENDIZAGEM
Aprendizagem:
Uma das propriedades mais importantes da RN é a capacidade de aprender por meio de exemplos e fazer inferências sôbre o que aprenderam, melhorando gradativamente o seu desempenho.As RN utilizam um algoritimo de aprendizagem, cuja tarefa é ajustar as formas de conexões.
Aprendizado supervisionado:
Um agente externo(professor) apresenta a rede alguns conjuntos de padrões de entrada e saida.
Portanto é necessário ter um conhecimento prévio do que se deseja ou se espera da rede.
Para cada entrada o professor indica explicitamente se a resposta calculada é boa ou ruim.
A resposta fornecida pela rede neural é comparada a resposta esperada.
O erro verificado é informado a rede para que sejam feitos ajustes a fim de melhorar suas futuras respostas.
Exemplo.:
Aprendizado por Reforço:
para cada entrada apresentada, é produzida uma indicação (reforço) sobre a adequação das saídas correspondentes produzidas pela rede.
Aprendizado Não-supervisionado:
`A rede atualiza seus pesos sem o uso de pares entrada-saídas desejadas e sem indicações sobre a adequação das saídas produzidas.
AUTOMATA
Maquina de estado
Ou autômato finito é uma modelagem de um comportamento composto por estados, transições e ações.
É um sistema sequencial de estados finitos.
Um estado armazena informações sobre o passado
.
Um estado muda a cada momento. Ex: conta paga, copo cheio dágua, geladeira aberta, interruptor ligado, etc
Uma transição indica uma mudança de estado ocorre qdo acontece algum evento intrno ou externo ao sistemae é descrita por uma condição que precisa ser realizada para que a transição ocorra.
Uma transição pode ser rotulada como uma epressão:
evento (lista-parâmetros) [guarda] / ação.
Uma ação é a descrição de uma atividade que deve ser realizada em determinado momento.
As entrada e saídas são consideradas em instantes de tempo discretos que são definidos por pulsos de um sinal de sincronização chamado relógio (clock).
As máquinas de estados são classificados de acordo com o tipo de função de saída, em dois tipos:
Máquina de Mealy e Máquina de Moore
A máquina de Mealy é um sistema seqüencial cuja saída no tempo t depende do estado e da entrada no tempo t, ou seja:
z(t) = H(s(t), x(t))
A máquina de Moore é um sistema seqüencial cuja saída no tempo t depende somente do estado no tempo t, ou seja:
z(t) = H(s(t))
Máquina de Moore:
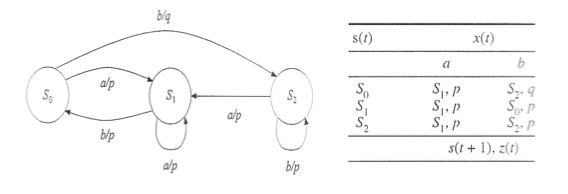 Máquina de Mealy:
Máquina de Mealy:
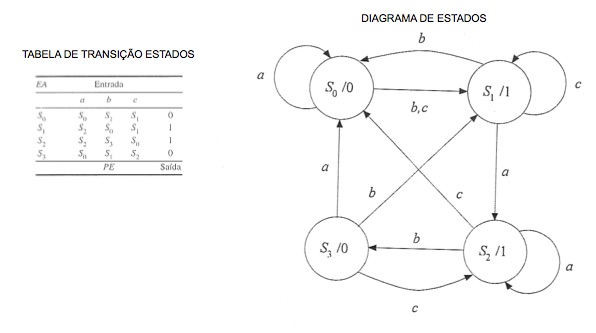
CIÊNCIA DA COMPUTAÇÃO
Contexto do aprendizado de máquina na ciência da computação
 ANÁLISE
Conceito de análise
ANÁLISE
Conceito de análise
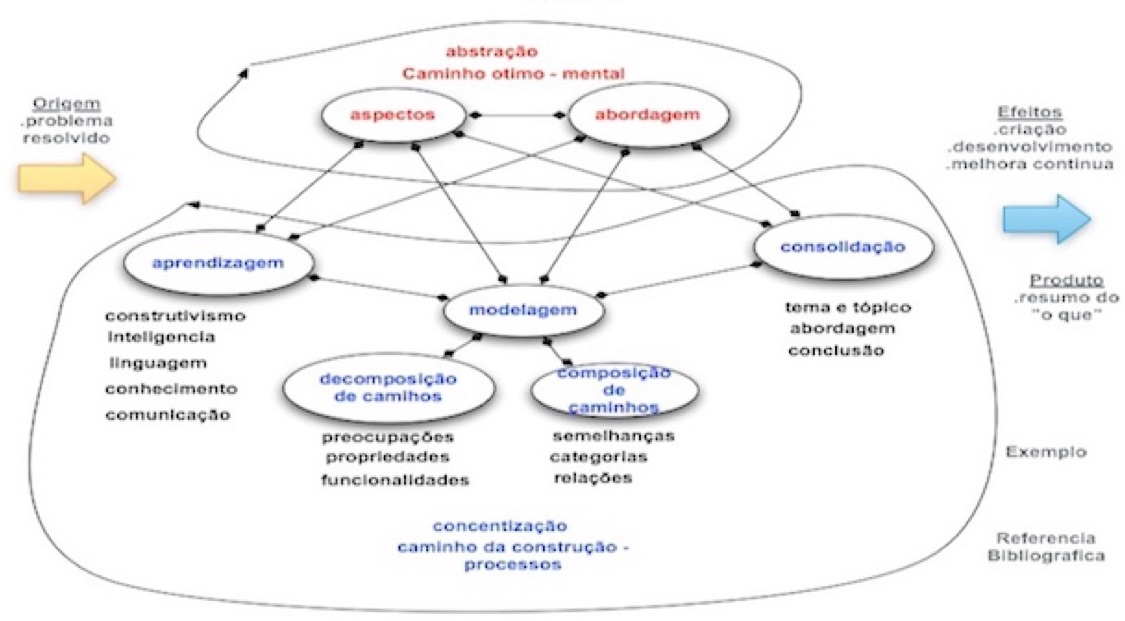 Visualização
Português
Relacionamento de tópicos em português
Frase -- periodo -- palavra -- função da palavra
Função da palavra -- Substantivo, verbos, adjetivos, preposição e termos
Termo -- essencial -- Sujeito e Predicado(verbo + algo sobre sujeito)
Termo -- integrante -- complemento verbal e nominal
Ex: Sujeito e predicado são termos (palavras de um periodo de uma oração) de uma frase.
Visualização
Português
Relacionamento de tópicos em português
Frase -- periodo -- palavra -- função da palavra
Função da palavra -- Substantivo, verbos, adjetivos, preposição e termos
Termo -- essencial -- Sujeito e Predicado(verbo + algo sobre sujeito)
Termo -- integrante -- complemento verbal e nominal
Ex: Sujeito e predicado são termos (palavras de um periodo de uma oração) de uma frase.
 Biblioteca
Biblioteca
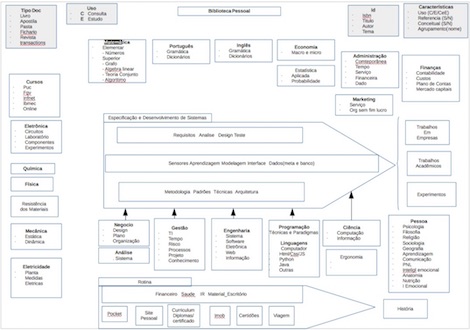 voltar ao topo
voltar ao topo
13. Referências:
São links de tópicos que foram utilizados para a obtenção do glossário.
Algoritmo perceptron e rede neurais - slides
- perceptron - exemplo seres vivos
- perceptron - resumo
- perceptron - detalhe
- modelos de rede
- Alguns Algoritmos de Aprendizado Supervisionado .
- rede neurais artificiais
- github - programa em python 3 implementação algoritmo
Aprendizado dos dados e inteligencia artificial - Livros, cursos e pdf's
- Livro - Abu-Mostafa,.... Learning from data. A short course
- indice dos cursos de aprendizado de dados
- Aprendizado como solução - video
- Aprendizado como solução - slide
-
Livro - Luger, George F. Inteligencia Artificial, 6 Ed, Person, 2013
Visualização
-
Trabalho sobre visualização para curso de Visualização da --- FGV-Emap
Modelagem e mineração de dados
-
Trabalho sôbre uso de ferramenta estatística (WEKA v 3-9-0 curso de Modelagem e Mineração de dados da --- FGV-Emap
Html e Css - texto cientifico
-
Math em Html e Css
-
Estrutura padrão de Código do html 5
-
Cheat Sheet Html5
Ambiente de desenvolvimento
-
Jupyter , Anaconda e Jupyter Notebook
-
Markdown O que é Markdown
Editor de texto científico
Latex
-
Acentuação das letras
- https://pt.wikipedia.org/wiki/Ajuda:Guia_de_edição/Fórmulas_TeX
- pt.wikibooks.org/wiki/Ajuda:Marcação_TeX#Sintaxe
-
codigo de caracteres html5
editor de formulas
-
Editor de formula matemática
-
introdução ao latex 2001
introdução ao latex 2006
Maquina de estado (autômata)
- Maquina de estados
Sistemas inteligentes coletivo
- Programando a inteligencia coletiva Segaran, Toby
Rede neural
- Rede neural artificial - Fundamentos Livro
- Rede neural artificial - wikipedia
- Rede neurais artificiais
-
Associação brasileira de inteligencia computacionaln
-
Aplicação aprendizado não supervisionado
Matemática
-
Função Afim
-
Desenho do grafico da função y=f(x)=2x-1
-
Função Afim
-
Equações
- Grafos - uma introdução
- Sociedade brasileira de matamática
Matemática Discreta
-
Matemática Discreta. L. Lovász, J. Pelikán e K. Vesztergombi.
-
-
Para computação e informática. Menezes, Paulo Blauth.
-
Algebra
-
Algebra e aplicações
-
Algebra Linear Poole, David
Estatistica
- Introdução a estatistica
Trilha de aprendizado para analise dados
Linguagem python
- Curso de verão Fgv introdução ao Python 3
-
algoritimo perceptron em python
Software
- Desenho
Draw da suite LibreOffice - livre
- Editor de programa
Sublime text para Mac-OS
voltar ao topo







 Formato de expressão matemática
Formato de expressão matemática



 Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: sub conjunto de B que é representado pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: sub conjunto de B que é representado pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
 Exemplo:
Exemplo:


 Um conjunto de n conexões
Um conjunto de n conexões  Máquina de Mealy:
Máquina de Mealy:


 Visualização
Português
Visualização
Português

 voltar ao topo
voltar ao topo